Given: A woman invests $6300 in an account that pays 6% interest per year, compounded continuously.
Required: a) To determine the amount after 2 years.
b) To determine how long it will take for the amount to be $8000.
Step-by-step explanation: The amount, A after t years with an interest rate of r is given by-
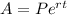
Here,
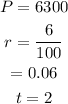
Substituting the values, we get-
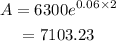
Hence the amount after 2 years is $7103.23
Next, let t be the time it takes for the amount to be $8000-
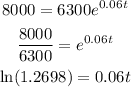
Further solving for t as-
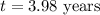
Hence, it takes 3.98 years for the amount to be $8000.
Final Answer: a) $7103.23
b) 3.98 years