Question

The item to the trashcan. Click the trashcan to clear all your answers.

Factor completely, then place the factors in The proper location on the grid.3y2 +7y+4

Answer 1

We are asked to factor in the following expression:

`3y^2+7y+4`

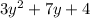
To do that we will multiply by 3/3:

`3y^2+7y+4=(3(3y^2+7y+4))/(3)`

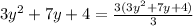
Now, we use the distributive property on the numerator:

`(3(3y^2+7y+4))/(3)=(9y^2+7(3y)+12)/(3)`

Now we factor in the numerator on the right side in the following form:

`(9y^2+7(3y)+12)/(3)=((3y+\cdot)(3y+\cdot))/(3)`

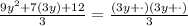
Now, in the spaces, we need to find 2 numbers whose product is 12 and their algebraic sum is 7. Those numbers are 4 and 3, since:

`\begin{gathered} 4*3=12 \\ 4+3=7 \end{gathered}`

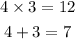
Substituting the numbers we get:

`((3y+4)(3y+3))/(3)`

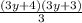
Now we take 3 as a common factor on the parenthesis on the right:

`((3y+4)(3y+3))/(3)=((3y+4)3(y+1))/(3)`

Now we cancel out the 3:

`((3y+4)3(y+1))/(3)=(3y+4)(y+1)`

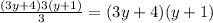
Therefore, the factored form of the expression is (3y + 4)(y + 1).