To solve the exercise, it is convenient to first draw a picture of the situation posed by the statement:
As you can see, a right triangle is formed. So to find the height at which the plane was when the pilot had flown one kilometer, you can use the trigonometric ratio sin(θ):
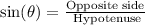
Then, in this case, you have

Therefore, the altitude or height of the plane after flying one kilometer is 358 meters.