Question

The equation 4.05p + 14.40 = 4.50(p +3) represents the number p of pounds of peanuts you need to make trail mix. How many pounds of peanuts do you need for the trail mix?

Answer 1

The equation given is a one variable equation, "p".

The question asks to find the value of "p", which is the pounds of peanuts.

So, we need to solve the euqation for "p".

`4.05p+14.40=4.50(p+3)`

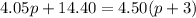
First, we need to put all the terms that have "p" in one side. For this, we will have to use the distributive property in the parenthesys first:

`\begin{gathered} 4.05p+14.40=4.50p+4.50\cdot3 \\ 4.05p+14.40=4.50p+13.50 \end{gathered}`

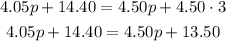
Now, we can substract 4.05p in both sides to get the "p" term of the left to the right:

`\begin{gathered} -4.05p+4.05p+14.40=-4.05p+4.50p+13.50 \\ 14.40=(4.50-4.05)p+13.50 \\ 14.40=0.45p+13.50 \end{gathered}`

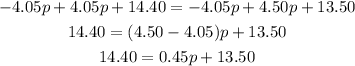
Now, we do the same for the 13.50, substract it in both sides:

`\begin{gathered} 14.40-13.50=0.45p+13.50-13.50 \\ 0.9=0.45p \\ 0.45p=0.9 \end{gathered}`

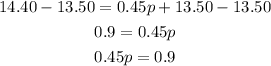
Now, we can divide both sides by 0.45:

`\begin{gathered} (0.45p)/(0.45)=(0.9)/(0.45) \\ p=2 \end{gathered}`

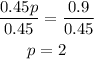
So, the answer is p = 2, thus, you need 2 pounds of peanuts for the trail mix.