We know that
• The mean is 200 pounds.
,
• The standard deviation is 25 pounds.
,
• The random sample is 35.
First, let's find the Z value using the following formula
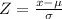
Let's replace the mean, the standard deviation, and x = 210.
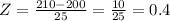
Then, using a p-value table associated with z-scores, we find the probability
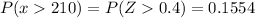
Therefore, the probability is 0.1554.
The table used is shown below