Question

Show that if the diagonals of a quadrilateral bisect each other at right angles then it is a rhombus.

Answer 1

To Show that if the diagonals of a quadrilateral bisect each other at right angles then it is a rhombus.

Proof:

Let ABCD be a quadrilateral such that the diagonals bisect each other,

Therefore,

`\begin{gathered} OA=OC\ldots(1) \\ OB=OD\ldots(2) \end{gathered}`

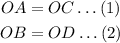
the diagonal bisect at right angle.

Hence,

`\begin{gathered} \angle AOB=90^(\circ) \\ \angle BOC=90^(\circ) \\ \angle COD=90^(\circ) \\ \angle AOD=90^(\circ)\ldots(3) \end{gathered}`

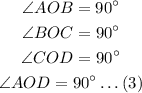
to prove: ABCD is rombus,

Rombus: its is a parallelogram, with all the sides equal.

so, to prove ABCD a parallelogram.

consider the triangle,

`\begin{gathered} triangleAOD\text{ and triangle }COB, \\ OA=OC \\ \angle AOD=\angle COB \\ OD=OB \\ \end{gathered}`

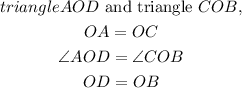
thus, traingle

`\text{AOD}\cong COB`

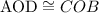
consider the sides, AD and BC

with the transversal ac,

The angles,

`\angle OAD\text{ AND }\angle OCB`

are alterntaive angles. they are equal.

this implies, AD is parallel BC.

similarly, AB is parallel to DC.

Hence, AD II BC and AB II DC.

In ABCD the opposite sides are parallel,

This implies, ABCD is parallelogram.

Now, to prove that ABCD is a rombus.

for that all the sides of ABCD should be equal.

now, consider the triangle AOD and COD.

`\begin{gathered} OA=OC \\ \angle AOD=\angle COD \\ OD=OD\text{ common side} \end{gathered}`

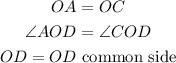
By SAS congruent rule,

Traingles,

`AOD\cong COD`

Thus, by CPCT Corresponding parts of congruent triangles ,

AD= CD

we know that,

AD=CB and CD=AB

Thus, AD=CD=CB=AB.

hence, all the sides are eqaul and ABCD is parallelogram.

So, ABCD is a rhombus.