Let m denote the number of minutes.
Plan A:
The customer pays a monthly fee of $30 and then an additional 9 cents per minute of use.
Mathematically,
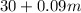
Plan B:
The customer pays a monthly fee of $33.60 and then an additional 8 cents per minute of use.
Mathematically,
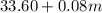
For what amounts of monthly phone use will Plan A cost less than Plan B?
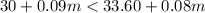
Let us solve the above inequality for m

This means that for less than 360 minutes, plan A will cost less than Plan B.