Question

Suppose 225 trout are seeded into a lake. Absent constraint, their population will grow by 25% a year. If the lake can sustain a maximum of 3500 trout, use a logistic growth model to estimate the number of trout after 5 years. trout

Answer 1

It is known that the population growth model is given by:

`P=P_0e^(kt)`

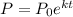
Initial population is 225 so P0=225 so it follows:

`P=225e^(kt)`

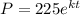
Each year the population will increase by 25% so it follows:

`\begin{gathered} P_0+0.25P_0=225e^k \\ e^k=(5)/(4) \\ k\ln e=\ln ((5)/(4)) \\ k\approx0.2231 \end{gathered}`

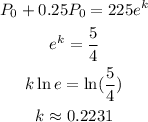
So the population function is:

`P=225e^(0.2231t)`

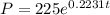
The population in 5 years is given by:

`P=225e^(0.2231*5)\approx686.4960025`

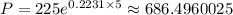
Hence the population of trout will be 686.4960025 after 5 years which can be rounded to 687.