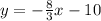From the question
We are given the points
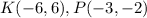
Finding the slopre, m
Slope is calculated using
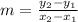
From the given points
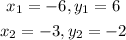
Therefore,
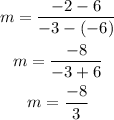
Therefore, m = -8/3
The next thing is to find
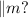
A slope parallel to m
For parallel lines, slopes are equal
Therefore,
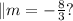
Next, we are to find

A slope perpendicular to m
For perpendicular lines, the product of the slopes = -1
Therefore
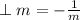
Hence,
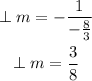
Therefore,

Next, we are to find the distance KP
Using the formula
![KP=\sqrt[]{(x_2-x_1)^2+(y_2-y_1)^2}](https://img.qammunity.org/2023/formulas/mathematics/college/3zxpk0psdw9cypzcw62zoijeehfk78xstq.png)
This gives
![\begin{gathered} KP=\sqrt[]{(-3-(-6))^2+(-2-6)^2} \\ KP=\sqrt[]{3^2+(-8)^2} \\ KP=\sqrt[]{9+64} \\ KP=\sqrt[]{73} \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/yggj853mdjj0emxa5prtvovj6maxzc07un.png)
Therefore,
![\text{Distance }=\sqrt[]{73}](https://img.qammunity.org/2023/formulas/mathematics/college/kskc3usc3cndbtm3k47lyo0zdxqncprdhp.png)
Next, equation of the line
The equation can be calculated using
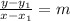
By inserting values we have

Therefore the equation is