Question

Precalc and i need help withb. Sec(18pie)c. Sin(7pie/6) tan(8pie/3)d. Tan(pie/12)

Answer 1

In b we need to find:

`\sec 18\pi`

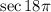
It's important to recal that the secant is equal to:

`\sec 18\pi=(1)/(\cos18\pi)`

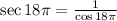
Another important property that will be useful is:

`\cos x=\cos (x+2\pi m)`

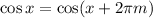
Where m is any integer. Let's see if we can write 18*pi using this. We can take x=0 so we have:

`\begin{gathered} 18\pi=x+2\pi m=2\pi m \\ 18\pi=2\pi m \end{gathered}`

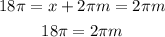
If we divide both sides by 2*pi:

`\begin{gathered} (18\pi)/(2\pi)=(2\pi m)/(2\pi) \\ 9=m \end{gathered}`

Since m is an integer then we can assure that:

`\cos 18\pi=\cos (0+2\pi\cdot9)=\cos 0=1`

Then the secant is given by:

`\sec 18\pi=(1)/(\cos18\pi)=(1)/(\cos 0)=1`

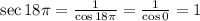
So the answer to b is 1.

In c we need to find:

`\sin ((7\pi)/(6))\tan ((8\pi)/(3))`

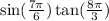
Here we can use the following properties in order to write those angles as angles of the first quadrant:

`\begin{gathered} \sin (x)=-\sin (x-\pi) \\ \tan (x)=\tan (x-m\pi)\text{ with }m\text{ being an integer} \end{gathered}`

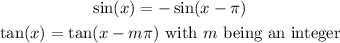
So we have:

`\begin{gathered} \sin ((7\pi)/(6))=-\sin ((7\pi)/(6)-\pi)=-\sin ((\pi)/(6)) \\ \tan ((8\pi)/(3))=\tan ((8\pi)/(3)-3\pi)=\tan (-(1)/(3)\pi) \end{gathered}`

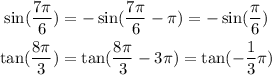
If we convert these two angles from radians to degrees by multiplying 360° and dividing by 2*pi we have:

`\begin{gathered} (\pi)/(6)\cdot(360^(\circ))/(2\pi)=30^(\circ) \\ -(1)/(3)\pi\cdot(360^(\circ))/(2\pi)=-60^(\circ) \end{gathered}`

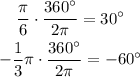
And remeber that:

`\tan x=-\tan (-x)`

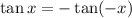
So we get:

`\begin{gathered} \sin ((7\pi)/(6))=-\sin ((\pi)/(6))=-\sin (30^(\circ)) \\ \tan ((8\pi)/(3))=\tan (-(\pi)/(3))=-\tan ((\pi)/(3))=-\tan (60^(\circ)) \end{gathered}`

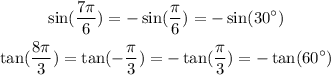
Then we can use a table of values:

Then:

`\sin ((7\pi)/(6))\tan ((8\pi)/(3))=\sin (30^(\circ))\cdot\tan (60^(\circ))=(1)/(2)\cdot\sqrt[]{3}=\frac{\sqrt[]{3}}{2}`

So the answer to c is (√3)/2.

In d we need to find:

`\tan ((\pi)/(12))`

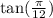
In order to do this using the table we can use the following:

`\begin{gathered} \tan x=(\sin x)/(\cos x) \\ \sin 2x=2\sin x\cos x \\ \cos 2x=\cos ^2x-\sin ^2x \\ \cos ^2x+\sin ^2x=1 \end{gathered}`

So from the first one we have:

`\tan ((\pi)/(12))=(\sin ((\pi)/(12)))/(\cos ((\pi)/(12)))`

We convert pi/12 into degrees:

`(\pi)/(12)\cdot(360^(\circ))/(2\pi)=15^(\circ)`

So we need to find the sine and cosine of 15°. We use the second equation:

`\begin{gathered} \sin 30^(\circ)=(1)/(2)=\sin (2\cdot15^(\circ))=2\sin 15^(\circ)\cos 15^(\circ) \\ \sin 15^(\circ)\cos 15^(\circ)=(1)/(4) \end{gathered}`

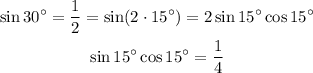
Then we use the third:

`\begin{gathered} \cos (30^(\circ))=\frac{\sqrt[]{3}}{2}=\cos (2\cdot15^(\circ))=\cos ^215^(\circ)-\sin ^215^(\circ) \\ \frac{\sqrt[]{3}}{2}=\cos ^215^(\circ)-\sin ^215^(\circ) \end{gathered}`

And from the fourth equation we get:

`\begin{gathered} \cos ^215^(\circ)+\sin ^215^(\circ)=1 \\ \sin ^215^(\circ)=1-\cos ^215^(\circ) \end{gathered}`

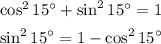
We can use this in the previous equation:

`\begin{gathered} \frac{\sqrt[]{3}}{2}=\cos ^215^(\circ)-\sin ^215^(\circ)=\cos ^215^(\circ)-(1-\cos ^215^(\circ)) \\ \frac{\sqrt[]{3}}{2}=2\cos ^215^(\circ)-1 \\ \cos 15^(\circ)=\sqrt{\frac{1+\frac{\sqrt[]{3}}{2}}{2}} \\ \cos 15^(\circ)=\sqrt{(1)/(2)+\frac{\sqrt[]{3}}{4}} \end{gathered}`

So we found the cosine. For the sine we use the expression with the sine and cosine multiplying:

`\begin{gathered} \sin 15^(\circ)\cos 15^(\circ)=(1)/(4) \\ \sin 15^(\circ)\cdot\sqrt[]{(1)/(2)+\frac{\sqrt[]{3}}{4}}=(1)/(4) \\ \sin 15^(\circ)=\frac{1}{4\cdot\sqrt[]{(1)/(2)+\frac{\sqrt[]{3}}{4}}} \end{gathered}`

Then the tangent is:

`\tan (15^(\circ))=(\sin(15^(\circ)))/(\cos(15^(\circ)))=\frac{1}{4\cdot\sqrt[]{(1)/(2)+\frac{\sqrt[]{3}}{4}}}\cdot\frac{1}{\sqrt[]{(1)/(2)+\frac{\sqrt[]{3}}{4}}}=(1)/(4)\cdot\frac{1}{(1)/(2)+\frac{\sqrt[]{3}}{4}}`

`\tan (15^(\circ))=(1)/(4)\cdot\frac{1}{(1)/(2)+\frac{\sqrt[]{3}}{4}}=\frac{1}{2+\sqrt[]{3}}`

Then the answer to d is:

`\frac{1}{2+\sqrt[]{3}}`