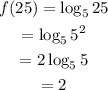Given:
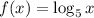
Required: Function values at x = 1/5, 1, 5, and 25.
Step-by-step explanation:
Use the logarithmic properties
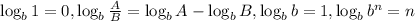
To find f(1/5), substitute 1/5 for x into f(x).
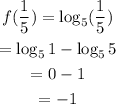
To find f(1), substitute 1 for x into f(x).
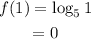
To find f(5), substitute 5 for x into f(x).
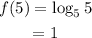
To find f(25), substitute 25 for x into f(x).