Question

The Arnold Inn offers two plans for wedding parties. Under plan A, the inn charges $30 for each person in attendance. Under plan B, the inn charges $1300 plus $20 for each person in excess of the first 25 who attend. For what size parties will plan B cost less? I do not understand how for Plan b: 1300+20(p-25). I do not understand the part p-25

Answer 1

81 people

Step-by-step explanation

Let p be the number of people that attend the party.

Under plan A, the inn charges $30 for each person, so the value y of a party for p people is,

`y_A=30x`

Then, under plan B, the cost is $1300 for a maximum of 25 people - this means that if 1 to 25 people attend the party, the cost is the same, $1300. For each person in excess of the first 25 - this means for 26, 27, 28, etc, the inn charges $20 each. The cost for plan B is,

`y_B=1300+20(p-25)`

The last part, (p - 25), is the part of the equation that separates the first 25 attendees. This equation works for 25 people or more, but it is okay to solve this problem. Note that for p = 25, the cost for plan A is,

`y_A=30\cdot25=750`

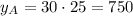
Which is less than the cost of plan B ($1300).

We have to find for what number of people attending the party, the cost of plan B is less than the cost of plan A,

`y_BThis is,[tex]1300+20(p-25)<30p`

We have to solve this for p. First, apply the distributive property of multiplication over addition/subtract4ion to the 20,

`\begin{gathered} 1300+20p-20\cdot25<30p \\ 1300+20p-500<30p \end{gathered}`

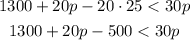
Add like terms,

`\begin{gathered} (1300-500)+20p<30p \\ 800+20p<30p \end{gathered}`

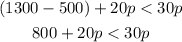
Now, subtract 20p from both sides,

`\begin{gathered} 800+20p-20p<30p-20p \\ 800<10p \end{gathered}`

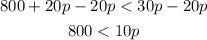
And divide both sides by 10,

Both have the same cost. The solution to the inequation was the number of people, p, is more than 80. This means that for 81 people the cost of plan B should be less than the cost of plan A,

`\begin{gathered} y_A=30\cdot81=2430 \\ y_B=1300+20(81-25)=2420 \end{gathered}`

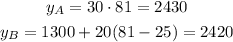
For 81 people, plan B costs $10 less than plan A.