Question

Y = x2 + 5x - 10y=-x² + 2x + 10

Answer 1

Since in both given equations, the variable y is already clear, then you can equal the two equations and then solve for x. So, you have

`\begin{cases}y=x^2+5x-10\text{ (1)} \\ y=-x^(2)+2x+10\text{ (2)}\end{cases}`
`\begin{gathered} x^2+5x-10=-x^2+2x+10 \\ \text{ Add }x^2\text{ to both sides of the equation} \\ \text{ Subtract 2x to both sides of the equation} \\ \text{ Subtract 10 to both sides of the equation} \\ x^2+5x-10+x^2-2x-10=-x^2+2x+10+x^2-2x-10 \\ 2x^2+3x-20=0 \end{gathered}`

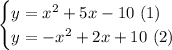
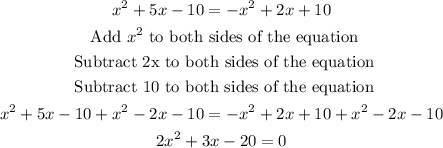
To solve for x you can use the quadratic formula, that is,

`\begin{gathered} \text{ For }ax^2+bx+c=0\text{ where a}\\e0 \\ x=\frac{-b\pm\sqrt[]{b^2-4ac}}{2a} \end{gathered}`

In this case

a=2

b=3

c=-20

So,

`\begin{gathered} x=\frac{-3\pm\sqrt[]{(3)^2-4(2)(-20)}}{2\cdot2} \\ x=\frac{-3\pm\sqrt[]{9+160}}{4} \\ x=\frac{-3\pm\sqrt[]{169}}{4} \\ x=(-3\pm13)/(4) \\ x_1=(-3+13)/(4)=(10)/(4)=(5)/(2)=2.5 \\ x_2=(-3-13)/(4)=(-16)/(4)=-4 \end{gathered}`

Now you can plug in the solutions found in any of the given equations to find their respective y-coordinates.

For the first solution, you have

`\begin{gathered} x_1=(5)/(2) \\ y_{}=-x^2+2x+10\text{ (2)} \\ y_1=-((5)/(2))^2+2((5)/(2))+10 \\ y_1=-(25)/(4)+5+10 \\ y_1=(35)/(4) \\ y_1=8.75 \\ \text{ Then} \\ (2.5,8.75) \end{gathered}`

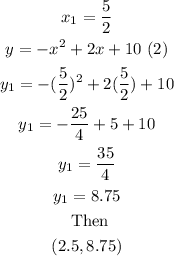
For the second solution, you have

`\begin{gathered} x_2=-4 \\ y=-x^2+2x+10\text{ (2)} \\ y_2=-(-4)^2+2(-4)+10 \\ y_2=-16-8+10 \\ y_2=-14 \\ \text{Then} \\ (-4,-14) \end{gathered}`

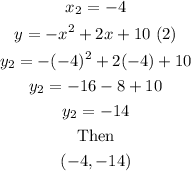
Therefore, the solution set of the given system of equations is

`\mleft\lbrace(-4,-14),(2.5,8.75)\mright\rbrace`