Answer:
• m=-2, b=-3
,
• m=-2, b=2
Step-by-step explanation:
The slope-intercept form of the equation of a line is:
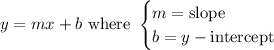
Part A
Given the equation:
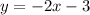
• The slope, m = -2
,
• The y-intercept, b=-3
Part B
Given the equation:
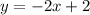
• The slope, m = -2
,
• The y-intercept, b=2