Question

A line that passes through the point (2,1) and is parallel to the line y = -2x + 5

Answer 1

A line in slope-intercept form is represented by the following equation:

`\begin{gathered} y=mx+b \\ \text{where,} \\ m=\text{slope} \\ b=y-\text{intercept} \end{gathered}`

Parallel lines have the same slope, then if the line is parallel to the line y=-2x+5, the slope of the parallel line would be -2 too.

Now, by the given point (2,1) and knowing the slope of the line, we can use the slope-point form of the line equation to get the slope-intercept form:

`\begin{gathered} y-y_0=m(x-x_0) \\ \text{where,} \\ (x_0,y_0)\text{ is the given point} \\ m\text{ is the slope} \end{gathered}`

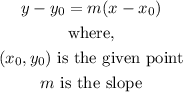
Substituting:

`\begin{gathered} y-1=-2(x-2) \\ y=-2x+4+1 \\ y=-2x+5 \end{gathered}`

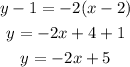
Notice that the parallel line would be the same original line, y=-2x+5.