Question

A train car with a mass of 5 kg and speed of 5 m/s is traveling to the right. Another train car with a mass of 2 kg is standing still. After the collision, the 5 kg train car is stuck to the 2 kg train car, what is their combined Final Velocity?

Answer 1

From the Law of Conservation of Linear Momentum, we have:

`m_1v_1+m_2v_2=m_1v_1^(\prime)+m_2v_2^(\prime)`

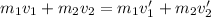
If the two particles have the same velocity after the collision, then v₁'=v₂'.

Let v be equal to the final velocity of the particles. Then:

`\begin{gathered} m_1v_1+m_2v_2=m_1v+m_2v \\ \\ \Rightarrow m_1v_1+m_2v_2=(m_1+m_2)v \end{gathered}`

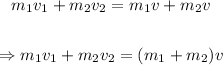
Since v is unknown, isolate it from the equation:

`v=(m_1v_1+m_2v_2)/(m_1+m_2)`

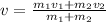
Replace the data to find the value of v:

`\begin{gathered} m_1=5kg \\ v_1=5(m)/(s) \\ \\ m_2=2kg \\ v_2=0 \\ \\ \Rightarrow v=((5kg)(5(m)/(s))+(2kg)(0))/(5kg+7kg)=(25kg(m)/(s))/(12kg)=2.08333...(m)/(s) \end{gathered}`

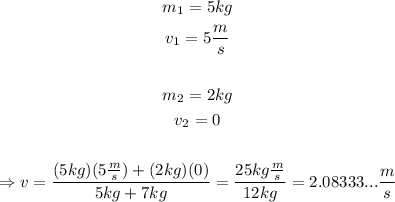
Therefore, the combined final velocity of both train cars is approximately 2.1m/s.