Answer:
Explanation:
Let us draw the pool for our visualization:
Pressure is defined as Force / area.
Now, what is the total force on the bottom of the pool?
It will be equal to the force due to the atmospheric pressure + force due to the mass of the water.
If we call p the density of water, then the force is
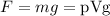
where V = volume of the pool.
Therefore, the pressure due to water is
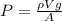
Here remember that V = abh and A = ab; therefore, the above gives
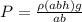
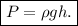
adding the atmospheric pressure gives
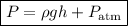
This is the pressure exerted on the bottom of the pool. But what about the sides?
Now near the bottom of the pool, the pressure exerted on the walls will be about the same as that exerted on the bottom of the pool. Therefore, we can use the above equation to find the pressure on the walls near the bottom.
SInce p = 1000kg / m^3, g = 9.8 m s^2, P_atm = 101325 Pascals, and h = 1.8 m, the equation gives
![P=(\frac{1000\operatorname{kg}}{m^3})*((9.8m)/(s^2))*(1.8m)+101325(N/m)]()
which evaluates to give
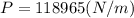
or in scientific notation, the above is
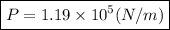
which is our answer!
Note that we also added to atmospheric pressure. This pressure will of course be canceled with the outside atmospheric pressure, leaving only the pressure due to water in effect.