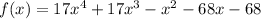
In order to identify bounds on the real zeros of this polynomial, first we need to find tendencies about the signal of f(x)
We know that the two term with highest degree is being multiplied by a positive coefficient. Therefore, we can initially conclude the f(x) tends to positive infinite as x grows either positive or negative.
We can check that, for x = -2, the first term is 272, and the remaining thermis togheter are given by:
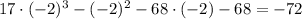
Then for x < -2, and for also for x > 2, we can state for sure that f(x) remains always positive.
Then, any possible roots must lies in the intervel (-2,2)
e can also chegck that, for x = 1, f(x) = -103, and, for x = -1, f(x) = -1.
Therefore, f(x) must have a root between