The given problem can be exemplified in the following diagram:
The conditions are:
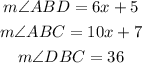
We also have the following relationship:
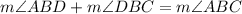
Substituting the values we get:
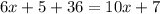
Solving the operations:
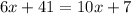
Now we solve for "x", first by subtracting 10x on both sides:
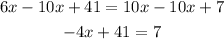
Now we subtract 41 on both sides:
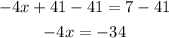
Now we divide both sides by -4
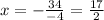
Now we replace the value of "x" in the expression for angle ABD:
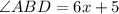
Replacing the value of "x":
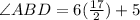
Solving the operations:
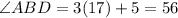
Therefore angle ABD is 56 degrees.