Let the number of history textbooks be h and the number of physics textbooks be p.
It was given that the bookstore sells a combined total of 347 books. Thus we have:
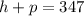
It is also given that the number of history textbooks sold was 79 more than the number of physics textbooks. This gives:
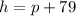
We can substitute for h into the first equation:
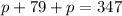
Solving, we have:
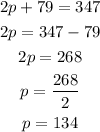
Substitute for p in the second equation, we have:
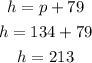
Therefore, there were 134 physics textbooks and 213 history textbooks.