To answer this question we will set and solve an equation.
Recall that the exterior angle of an n-gon has a measure of:
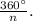
Let n be the number of sides that the polygon that we are looking for has. Since the regular polygon exterior angles with a measure of approximately 17.14 degrees, then:
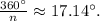
Therefore:
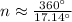
Simplifying the above result we get:
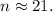
Answer: 21 sides.