Question

Frustratingly this is the third time I’m asking this question that two tutors got wrong. Please help?

Answer 1

To answer this question, we need to translate each of the expressions into algebraic form. Then we have:

1. We have that one number is 2 less than a second number.

In this case, let x be one of the numbers, and y the second number. Now, we can write the expression as follows:

`x=y-2`

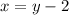
2. We also have that twice the second number is 2 less than 3 times the first:

`2y=3x-2`

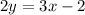
3. And now, we have the following system of equations:

`\begin{cases}x=y-2 \\ 2y=3x-2\end{cases}`

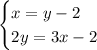
4. And we can solve by substitution as follows:

`\begin{gathered} x=y-2\text{ then we have:} \\ \\ 2y=3(y-2)-2 \\ \\ 2y=3(y)+(3)(-2)-2 \\ \\ 2y=3y-6-2 \\ \\ 2y=3y-8 \end{gathered}`

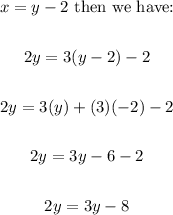
5. To solve this equation, we can subtract 2y from both sides, and add 8 from both sides too:

`\begin{gathered} 2y-2y=3y-2y-8 \\ 0=y-8 \\ 8=y-8+8 \\ 8=y \\ y=8 \end{gathered}`

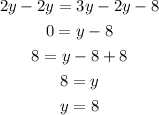
6. Since y = 8, then we can use one of the original equations to find x as follows:

`\begin{gathered} x=y-2\Rightarrow y=8 \\ x=8-2 \\ x=6 \end{gathered}`

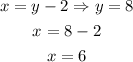
Therefore, we have that both numbers are x = 6, and y = 8.

In summary, we have that:

• The smaller number is 6.

,

• The larger number is 8.