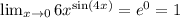Question

Limit using L'Hopital's rule . I just want to make sure if my answer is correct or not?

Answer 1

In order to use L'Hopital's rule, it is necessary to rewrite the limit as the quotient of two functions. Notice that:

`\begin{gathered} 6x^(\sin (4x))=e^{\ln (6x^(\sin (ex)))^{}} \\ =e^(\sin (4x)\cdot\ln (6x)) \end{gathered}`

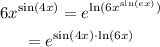
Since the exponential function is a continuous function, then:

`\lim _{\text{x}\rightarrow0}e^(\sin (4x)\cdot\ln (6x))=e^{\lim _(x\rightarrow0)\sin (4x)\cdot\ln (6x)}`

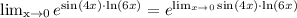
Find the following limit using L'Hopital's rule:

`\lim _(x\rightarrow0)\sin (4x)\cdot\ln (6x)`

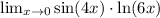
Write the function as a fraction:

`\lim _(x\rightarrow0)(\ln (6x))/(((1)/(\sin (4x))))`

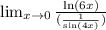
Use L'Hopital's rule to rewrite the limit as the limit of the quotient of the derivatives:

`\begin{gathered} \lim _(x\rightarrow0)(((1)/(x)))/((-(4\cos(4x))/(\sin^2(4x))))=\lim _(x\rightarrow0)-(\sin ^2(4x))/(4x\cdot\cos (4x)) \\ =\lim _(x\rightarrow0)\sin (4x)\cdot(\sin(4x))/(4x)\cdot(-1)/(\cos (4x)) \\ =\lim _(x\rightarrow0)\sin (4x)\cdot\lim _(x\rightarrow0)(\sin(4x))/(4x)\cdot\lim _(x\rightarrow0)(-1)/(\cos (4x)) \\ =0\cdot1\cdot-1 \\ =0 \end{gathered}`

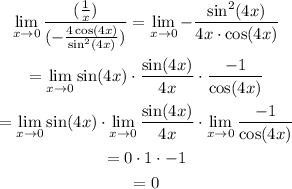
Therefore:

`\lim _(x\rightarrow0)6x^(\sin (4x))=e^0=1`