According to the given graph, the angles are linear pairs because they are on a straight angle, so the must sum 180°. Having said that, we express the following.-
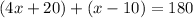
We reduce like terms
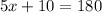
Then, we subtract 10 on each side.
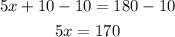
At last, we divide the equation by 5.
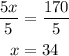
We use this value to find the angles.
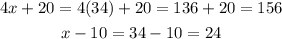
Therefore, x is equal to 34, and the angles are 156° and 24°.