Question

I need help on #13 please !!! Also with the (circle the vertex on the graph and draw the axis of symmetry) !

Answer 1

Given the quadratic equation

`2x^2-16x+24=0`

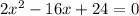
we want to solve for the vertex and its axis of symmetry.

To easily identify these properties of quadratic equation, we must put the equation first into its vertex form. The first step to write it in its vertex form is to move the constant on the right-hand side of the equation

`\begin{gathered} 2x^2-16x=-24 \\ x^2-8x=-12 \end{gathered}`

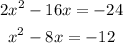
After that, we add the square of b/2 on the equation above. The value of b on the quadratic equation is -16. We have

`x^2-8x+((-8)/(2))^2=-12+((-8)/(2))^2`

Simplify the equation above

`\begin{gathered} x^2-8x+16=-12+16 \\ x^2-8x+16=4 \end{gathered}`

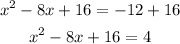
We write the expression on the left-hand side as perfect square, which is (x-4)^2.

`(x-4)^2=4`

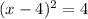
Transfer 4 to left-hand side to write the vertex form of the quadratic equation

`(x-4)^2-4=0_{}`

The vertex form has the general equation

`y=a(x-h)^2+k`

where (h,k) is the vertex of the parabola.

Based on the vertex form of the quadratic formula, the vertex exists at (4,-4). Also, the axis of symmetry is equal to h, which is in this case, equal to 4.

The representation of a vertex and axis of symmetry in a quadratic plot will be

Answer: Vertex = (4,-4)

Axis of symmetry = 4