We are given the following information
sin u = 5/13
cos v = -3/5
Where the angle u and v are in the 2nd quadrant.
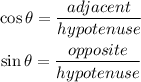
Let us find cos u
Apply the Pythagorean theorem to find the 3rd side.
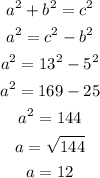
Cos u = 12/13
Now, let us find sin v
Apply the Pythagorean theorem to find the 3rd side.
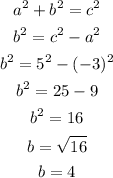
Sin v = 4/5
Recall the formula for sin (A - B)
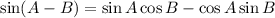
Let us apply the above formula to the given expression
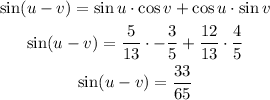
Therefore, sin (u - v) = 33/65