Given:
Mass of copper, m = 3.152 g = 0.003152 kg
Resistance = 2,473.562 ohms
Density of copper = 8900 kg/m³
Resistivity of copper = 1.7 x 10⁻⁸ ohm.m
Let's find the diameter of the wire.
Apply the density formula to find the volume:
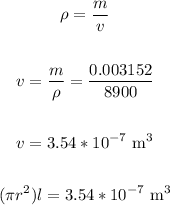
Now, apply the formula:
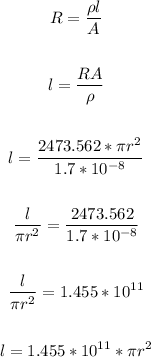
Now, combine both expressions for L:
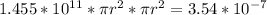
Solving further:
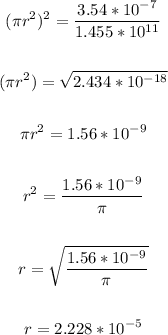
r is the radius.
We know that:
Diameter = 2 x radius
Thus, we have:
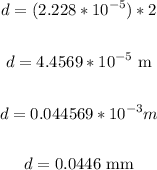
Therefore, the diameter in mm will be 0.0446 mm
ANSWER:
0.0446 mm