The definition of the inverse function is
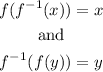
In our case,
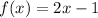
Then,
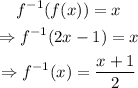
We need to verify this result using the other equality as shown below
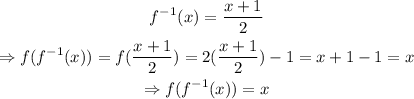
Therefore,
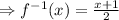
The inverse function is f^-1(x)=(x+1)/2.
We say that a relation is a function if, for x in the domain of f, there is only one value of f(x).
In our case, notice that for any value of x, there is only one value of (x+1)/2=x/2+1/2.
The function is indeed a function, it is a straight line on the plane that is not parallel to the y-axis.
The inverse f^-1(x) is indeed a function