Question

14. (04.06 LC)The first four terms of a sequence are shown below:8, 5, 2, -1Which of the following functions best defines this sequence? (5 points)f(1) = 8, f(n + 1) = f(n) + 5; forn 21f(1) = 8, f(n + 1) = f(n) - 5; for n 2 1f(1) = 8, f(n + 1) = f(n) - 3; for n 2 1f(1) = 8, f(n + 1) = f(n) + 3; forna 1

Answer 1

Given

The sequence, 8, 5, 2, -1.

To find: Which of the following functions best defines this sequence?

a) f(1) = 8, f(n + 1) = f(n) + 5; for n=1,2,3,4,...

b) f(1) = 8, f(n + 1) = f(n) - 5; for n=1,2,3,4,...

c) f(1) = 8, f(n + 1) = f(n) - 3; for n=1,2,3,4,...

d) f(1) = 8, f(n + 1) = f(n) + 3; for n=1,2,3,4,...

Step-by-step explanation:

It is given that,

The first four terms of a sequence is, 8, 5, 2, -1.

Since,

`\begin{gathered} 5-8=-3 \\ 2-5=-3 \end{gathered}`

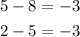
Then, the above sequence is an arithmetic sequence.

That implies,

`\begin{gathered} f(n)=f(1)+(n-1)d \\ =8+(n-1)(-3) \end{gathered}`

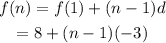
Therefore, for n=1,2.

`\begin{gathered} f(1)=8 \\ f(2)=8+(2-1)(-3) \\ =8-3 \\ =f(1)-3 \end{gathered}`

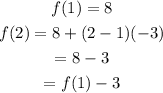
Then,

`f(n+1)=f(n)-3`

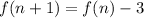
Final result: Hence, the answer is option c).