Question

2.) for the line represented by the given equation, find both the X intercept and the y-intercept. (Don’t simply look on the graphing calculator ). Make sure you indicate which answer is the x-intercept and which is the y-intercept . Then graph the line

Answer 1

To find the y-intercept, we substitute x=0 in the given equation:

`\begin{gathered} y=(1)/(2)\cdot0+3, \\ y=3. \end{gathered}`

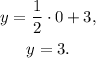
Therefore, the y-intercept has coordinates (0,3).

To find the x-intercept, we set y=0, and solve for x:

`\begin{gathered} 0=(1)/(2)x+3, \\ 0-3=(1)/(2)x+3-3, \\ -3=(1)/(2)x, \\ 2\cdot(-3)=2\cdot((1)/(2)x), \\ x=-6. \end{gathered}`

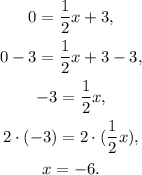
Therefore, the x-intercept has coordinates (-6,0).

Finally, the graph of the given equation is: