one solution: (1, 4)
The equations:
y = -x + 5
y = -5x + 9
Step-by-step explanation:
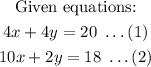
To plot the graphs, we can assign values to x. The we get the corresponding values of y for each of the equation.
Rewritting the two equations by making y the subject of formula:
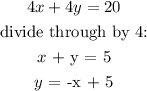
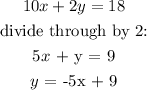
Plotting the graphs:
The point of intersection of the graphs is the solution.
There is one solution: (1, 4)