Question

Jay Field's bank granted him a single-payment loan of $6,800. He agreed to repay the loan in 91 days at an ordinary interest rate of 4.25 percent. What is the maturity value of the loan?

Answer 1

$6,872.05

Step-by-step explanation:

The maturity value of the loan can be calculated as:

`V=P(1+r\cdot t_{})`

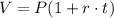
Where P is the initial amount, r is the interest rate as a decimal and t is the time in years.

4.25% is equivalent to: 4.25/100 = 0.0425

91 days are equivalent to 91/365 = 0.25 years

Then, the maturity value is equal to:

`\begin{gathered} V=6800(1+0.0425\cdot0.25) \\ V=6800(1+0.011) \\ V=6800(1.011) \\ V=\text{ \$6,872.05} \end{gathered}`

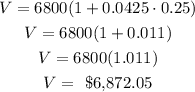
So, the maturity value of the loan is $6,872.05