We want to calculate the amount needed as an initial investment to have 120000 after 30 years.
Recall that the formula of annual compounding is given by the formula
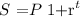
where P is the principal, r is the interest rate and t is the time in years. When compounded continously the formula is
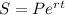
where the variables have the same meaning. In both cases we want to find P sucht that
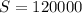
when t=30 and r is the interest rate that we are given.
So we have the following equation in the first case
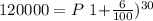
so if we divide both sides by (1+6/100)^30 we get
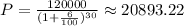
so for Plan A 20893.22 is needed to have 120000 after 30 years.
now, we want to do the same with the second plan. We have
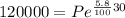
so we divide both sides by exp(5.8*30/100). So we get
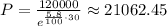
so for Plan B 21062.45 is needed to have 120000 after 30 years