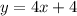First of all, remember that parallel lines are those with equivalent slope. So, the given line is
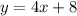
If the new line we have to find is parallel to this one, that means the slope is
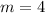
Because the coefficient of x is always the slope.
Now, we know that the new line must pass through (1,8) and it must have a slope of 4. We can use the point-slope formula

Replacing the point and the slope, we have
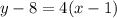
Then, we solve for y
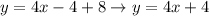
Therefore, the new parallel line is