Question

a) Form a suitable equation to show that x squared - 6x - 59 = 0b) Complete the square (x+p)squared-q= 0, and find the constants p and q.

Answer 1

Given:

There is a triangle given as

Required:

We want to find the sutiable form that show that

`x^2+6x-59=0`

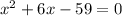
and also complete the square

`(x+p)^2-q=0`

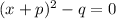
and find the value of p and q

Step-by-step explanation:

The area of triangle is

`\begin{gathered} (1)/(2)(x+1)(x+5)=32 \\ \\ x^2+5x+x+5=64 \\ x^2+6x-59=0 \end{gathered}`

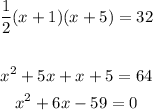
hence proved for a

Now for second

`\begin{gathered} x^2+6x+9-9-59=0 \\ (x+3)^2-68=0 \end{gathered}`

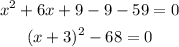
now compare with

`(x+p)^2-q=0`

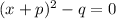
we get

`\begin{gathered} p=3 \\ q=68 \end{gathered}`

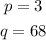
Final answer:

p=3 and q=68