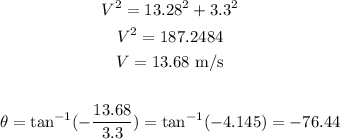a)
In order to calculate the required horizontal speed, first let's calculate the falling time, using the free-fall formula:
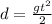
For d = 9 and g = 9.8, we have:
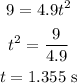
Then, let's use this time in the following formula for horizontal distance, so we can calculate the horizontal speed:
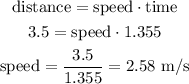
b)
Let's calculate the vertical velocity after 0.75 seconds, using the formula:
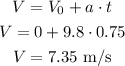
The magnitude can be calculated using the Pythagorean Theorem with the horizontal and vertical velocities:
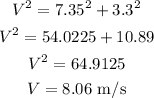
And the direction is given by the arc tangent of the vertical velocity divided by the horizontal velocity (for this, let's use a negative value of vertical velocity, since it points downwards)
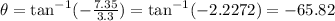
(d)
To find the vertical velocity, let's use Torricelli's equation:
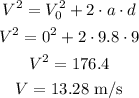
Calculating the final speed magnitude and orientation, we have: