a)
In order to calculate the frequency of oscillations of a simple harmonic oscillator, first let's calculate the period, using the formula:
![\begin{gathered} T=2\pi\sqrt[]{(m)/(k)} \\ T=2\pi\sqrt[]{(2)/(800)} \\ T=2\pi\sqrt[]{(1)/(400)} \\ T=2\pi\cdot(1)/(20) \\ T=(\pi)/(10)=0.31416\text{ s} \end{gathered}](https://img.qammunity.org/2023/formulas/physics/high-school/5rvualzopsnxy8wlh7gzysb3ovqoajds5d.png)
Since the frequency is the inverse of the period, we have:
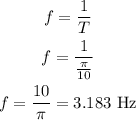
b)
In order to calculate the maximum oscillation amplitude given the maximum speed, let's use the formula below:
![\begin{gathered} v_(\max )=X\sqrt[]{(k)/(m)} \\ 10=X\cdot\sqrt[]{(800)/(2)} \\ 10=X\cdot20 \\ X=(10)/(20)=0.5\text{ meters} \end{gathered}](https://img.qammunity.org/2023/formulas/physics/high-school/bl4l5yfrtk0vlb9i66fphl96cier41gqpq.png)
c)
The formula for the pendulum frequency is:
![\begin{gathered} f=(1)/(T) \\ f=\frac{1}{2\pi\sqrt[]{(L)/(g)}} \\ f=\frac{\sqrt[]{(g)/(L)}}{2\pi} \end{gathered}](https://img.qammunity.org/2023/formulas/physics/high-school/37jog9ti6pnsivqhbfj3asp1s561mcuny1.png)
Then, for f = 3.183 and g = 9.81, we have:
![\begin{gathered} 3.183=\frac{\frac{\sqrt[]{9.81}}{\sqrt[]{L}}}{2\pi} \\ \frac{\sqrt[]{9.81}}{\sqrt[]{L}}=3.183\cdot2\pi \\ \frac{3.132}{\sqrt[]{L}}=20 \\ \sqrt[]{L}=(3.132)/(20) \\ \sqrt[]{L}=0.1566 \\ L=0.3957 \end{gathered}](https://img.qammunity.org/2023/formulas/physics/high-school/ifo3j4lcuti3ol56f2v4tbh1ew72zn11bu.png)
So the length is 0.3957 m or 39.57 cm.