Question

y=f(x) is the particular solution to the differential equation dy/dx=(x(y-1))/4, with the initial condition of f(1)=3. write an equation for the line tangent to the graph of f at the point (1,3) and use it to approximate f(1,4)

Answer 1

We are given the following differential equation:

`(dy)/(dx)=(x(y-1))/(4)`

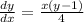
Since this equation gives the value of the slope of the tangent line at any point (x,y). To determine the equation of such line we need to use the general form of a line equation:

`y=mx+b`

Since in a tangent line the slope is equivalent to the derivative we may replace that into eh line equation like this:

`y=(dy)/(dx)x+b`

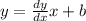
Now we determine the value of dy/dx at the point (1,3):

`(dy)/(dx)=((1)(3-1))/(4)=(2)/(4)=(1)/(2)`

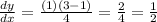
Replacing into the equation of the line:

`y=(1)/(2)x+b`

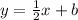
Now we replace the point (1,3) to get the value of "b":

`3=(1)/(2)(1)+b`

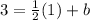
Solving for "b":

`\begin{gathered} 3=(1)/(2)+b \\ 3-(1)/(2)=b \\ (5)/(2)=b \end{gathered}`

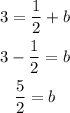
Replacing into the line equation:

`y=(1)/(2)x+(5)/(2)`

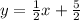
And thus we get the equation of the tangent line.

To approximate the value of f(1.4) we replace the value x = 1.4 in the equation of the tangent line:

`y=(1)/(2)(1.4)+(5)/(2)`

Solving the operation:

`y=3.2`

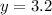
Therefore, the approximate value of f(1.4) is 3.2