Sally's wallet contains the following coins
Quarters = 5
Dimes = 3
Nickels = 8
Pennies = 4
What is the probability that she will choose a dime and then a quarter?
Recall that the probability of an event is given by
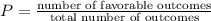
The probability that she will choose a dime is given by
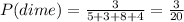
The probability that she will choose a quarter is given by
(note that replacement is allowed so the total number of coins remains the same)
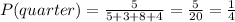
So, the probability that she will choose a dime and then a quarter is
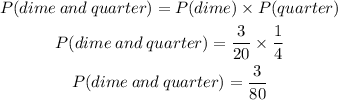
Therefore, the probability that she will choose a dime and then a quarter is 3/80