the shaft must have 4 inches of diameter
Step-by-step explanation
Step 1
given that The horsepower (hp) that a shaft can safely transmit varies jointly with its speed (in revolutions per minute, rpm) and the cube of its diameter.
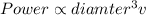
so
a) If a shaft of a certain material 2 inches in diameter can transmit 36 hp at 75 rpm
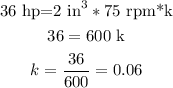
b)what diameter must the shaft have in order to transmit 134 hp at 35 rph
![\begin{gathered} Power\propto diamter^3v \\ Power=d^3*v*k \\ replace \\ 134=d^3*35*0.06 \\ 134=d^3*2.1 \\ divide\text{ both sides by 2.1} \\ (134)/(2.1)=(d^3*2.1)/(2.1) \\ 63.80=d^3 \\ cubic\text{ root in both sides} \\ \sqrt[3]{63.80}=\sqrt[3]{d^3} \\ 3.996=d \\ rounded \\ d=4\text{ inches} \end{gathered}](https://img.qammunity.org/2023/formulas/physics/college/6xatgi0a5mchegz83kwr8w4c3frfso5mqu.png)
therefore
the shaft must have 4 inches of diameter
I hope this helps you