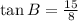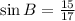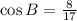To answer this question we need to remember the definition of the trigonometric functions:
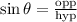
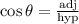
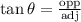
where opp denotes the opposite leg of the angle, adj the adjacent leg of the angle and hyp the hypotenuse.
Now, in this triangle we notice that for angle B the opposite leg is 15, the adjacent leg is 8 and the hypotenuse is 17. Plugging this values into the definitions above we have that: