Question

EFHNm FG=97m GH=117m EHG= 164GoAngle E:OAngle F:Angle G:Angle H:Blank 1:Blank 2:Blank 3:Blank 4:

Answer 1

Given a cyclic quadrilateral

As shown:

The measure of the arc FG = 97

The measure of the arc GH = 117

The measure of the arc EHG = 164

The measure of the arc is two times the measure of the inscribed angle opposite to the arc.

So, the measure of the angle E = 1/2 the measure of the arc FGH =

`(1)/(2)(\text{arc FG + arc GH ) =}(1)/(2)(97+117)=(1)/(2)\cdot214=107\degree`

The measure of the angle F = 1/2 the measure of the arc EHG =

`(1)/(2)\cdot164=82\degree`

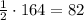
For the cyclic quadrilateral, every two opposite angles are supplementary.

So,

`\begin{gathered} m\angle E+m\angle G=180 \\ m\angle G=180-m\angle E=180-107=73\degree \end{gathered}`

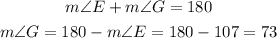
And:

`\begin{gathered} m\angle F+m\angle H=180 \\ m\angle H=180-m\angle F=180-82=98\degree \end{gathered}`

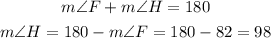
So, the answer will be:

`\begin{gathered} \text{Blank}1\colon107\degree \\ \text{Blank}2\colon82\degree \\ \text{Blank}3\colon73\degree \\ \text{Blank}4\colon98\degree \end{gathered}`