Question

9. Leyla has 18 50-cent and 20-cent coins altogether. She has a total of $6.90. How many 20-cent coins does she have?

Answer 1

According to the information given in the exercise:

- Leyla has 18 coins of 50 cents and 20 cents.

. She has a total of $6.90.

Let be "f" the number 50-cent coins and "t" the number 20-cent coins.

Since 1 dollar is equal to 100 cents, you know that:

`6.90dollars=690cents`

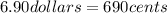
Then, knowing the above, you can set up the following System of Equations:

`\begin{cases}f+t=18 \\ \\ 50f+20t=690\end{cases}`

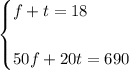
To find the value of "t", you can apply the Substitution Method:

1. Take the first equation and solve for "f":

`f=18-t`

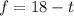
2. Substitute this equation into the second equation and solve for "t":

`\begin{gathered} 50f+20t=690 \\ \\ 50(18-t)+20t=690 \end{gathered}`
`\begin{gathered} 50(18-t)+20t=690 \\ \\ 900-50t+20t=690 \end{gathered}`
`\begin{gathered} 900-30t=690 \\ \\ -30t=690-900 \\ \\ -30t=-210 \end{gathered}`
`\begin{gathered} t=(-210)/(-30) \\ \\ t=7 \end{gathered}`

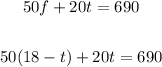
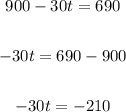
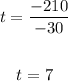
Therefore, the answer is: She has 7 coins of 20 cents.