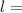Question

Solve the formula for the indicated variable.surface area of cone; S=r^2+rl; solve for l.

Answer 1

Given:

The formula for the surface area of the cone is given as,

`\begin{gathered} S.A\text{ = }\pi r^2+\pi rl \\ \end{gathered}`

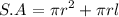
Required:

The modified formula for the surface area of the cone in terms of l.

Step-by-step explanation:

The formula is given as,

`S=\pi r^2+\pi rl`

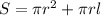
Taking common terms separately,

`\begin{gathered} S\text{ = }\pi r(r\text{ + l\rparen}_{\text{ }} \\ \end{gathered}`

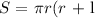
Transposing the common terms to LHS,

`r\text{ + l = }(S)/(\pi r)`

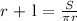
Rearranging the equation for l,

`\begin{gathered} l\text{ = }(S)/(\pi r)\text{ - r} \\ l\text{ = }(S-\pi r^2)/(\pi r) \end{gathered}`

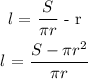
Answer:

Thus the required expression in terms of l is,

`l=\frac{\text{S-\pi r}^2\text{{}}}{\text{\pi r}}`