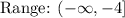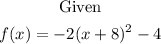
Since the given is a polynomial with a degree of 2, there are no restrictions to its domain. The domain therefore is

The given function is in the vertex form
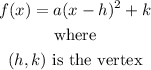
By inspection, we determine that the vertex of the function is at (-8,-4), and since a = -2, then the parabola opens up downwards. This implied that its output peaks at y = -4, and the graph continues towards negative infinity.
We can conclude therefore that the range is