Answer:
To solve the system of equations,
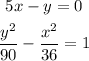
Solving 1st equation we get,
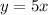
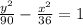
Substitute y=5x in the above equation, we get
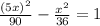
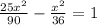
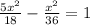

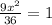
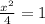
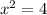

when x=2, we get y=5x=5(2)=10
when x=-2, we get y=5x=5(-2)=-10
There are two solution for the given system.
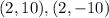
Answer is: x=2,y=10 and x=2,y=-10