Answer:
6.33 years
Explanation:
The formula for investment at compound interest is given below::
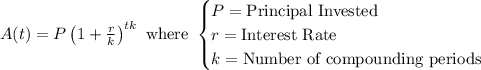
From the statement of the problem:
• The initial investment, P = $2500
,
• Annual Interest Rate, r = 7.5% = 0.075
,
• Compounding Period (Quarterly), k = 4
,
• Amount after t years, A(t) = $4000
,
• Time, t = ?
Substitute these values into the compound interest formula above:
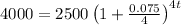
We then solve the equation for the value of t.
![\begin{gathered} \begin{equation*} 4000=2500\left(1+(0.075)/(4)\right)^(4t) \end{equation*} \\ \text{ Divide both sides by 2500} \\ (4000)/(2500)=\left(1+0.01875\right)^(4t) \\ 1.6=\left(1.01875\right)^(4t) \\ \text{ Take the log of both sides} \\ \log(1.6)=\log(1.01875)^(4t) \\ \text{ By the power law of logs, }\log a^n=n\log a \\ \log(1.6)=4t\log(1.01875) \\ \text{ Divide both sides by 4}\log(1.01875) \\ \frac{\operatorname{\log}(1.6)}{4\operatorname{\log}(1.01875)}=\frac{4t\operatorname{\log}(1.01875)}{4\operatorname{\log}(1.01875)} \\ t\approx6.33\text{ years} \end{gathered}]()
It will take approximately 6.33 years for a $2500 investment to grow to $4000.