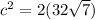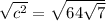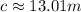Answer: 13.01m
Step-by-step explanation
A right triangle is a triangle with a 90º angle. If the square lot is divided by a diagonal, then two right triangles are formed:
The right triangle satisfies the Pythagorean Theorem:

where c is the diagonal (hypotenuse), and a and b are the sides. In our case, as it is a square, a = b, meaning:

Thus, simplifying and solving for c we can find the diagonal: