Question

Hi i have uploaded the question in the image. Equation no. 2 (ii).

Answer 1

Let's determine if g(x) is a factor of f(x).

`\text{ f(x) }=\text{ }x^3\text{ }-3x^2+4x-4`
`\text{ g(x) = }x\text{ - 2}`

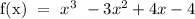
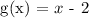
Given that g(x) = x - 2, at x = 2, let's check the value of f(x) at x = 2, If f(x) = 0, then g(x) is a factor, otherwise, g(x) is not a factor of f(x).

We get,

At x = 2,

`\begin{gathered} \text{ f(x) }=\text{ }x^3\text{ }-3x^2+4x-4 \\ \text{ f(2) = (2)}^3-3(2)^2\text{ + 4(2) - }4 \\ \text{ f(2) = 8 - 12 + 8 - }4 \\ \text{ f(2) = 16 - 1}6 \\ \text{ f(2) = 0} \end{gathered}`

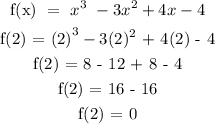
Therefore, g(x) is a factor of f(x).