Given: The coordinates of triangle ABC as
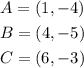
To Determine: The coordinates of triangle ABC after first reflect over the y-axis and then over the x-axis
Solution
The reflection over the y-axis rule is given as
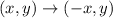
Let us apply the rule to the given triangle ABC
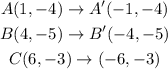
The reflection rule over the x-axis is given as
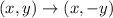
Let us apply the rule to the given
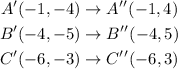
Hence, the new point of A'' = (-1, 4)